今天舒兵课末讲了一个“完全无匹配”问题(即有N个对象A和N个对象B分别编号 1,2,3,…,N ,A与B一一组合,要求A与B编号不相同),于是全班陷入了通式计算的苦战中..
在又报废两页草稿纸之后终于得出一个好吓人的通式:
大致意思是这样:首先求出包括任何匹配的所有情况,然后减去匹配1对的总数,减去2对的,……,减去N对的,最后的结果就是完全无匹配的总数。但是由于计算N对的时候仍然需要用到一个更小范围的完全无匹配,因此这个算法变成了递归算法,只能用计算机求解了。
代码编写上增加了一个缓存,防止重复运算,毕竟输入唯一值输出也是唯一值,而且运算量很可观。
以下是在线计算。注意:由于运算位数不够最高只能求到170,并且23及以上只能用指数方法表示浮点数。
请在上方输入要运算的完全无匹配对象的总数
2016.10.27 更新:通解记作 !n (Derangement/subfactorial) 更简单的递推公式见 http://www.matrix67.com/blog/archives/6665 第二题.

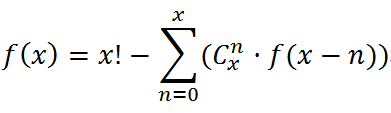

0 条评论。